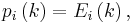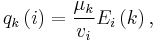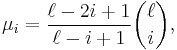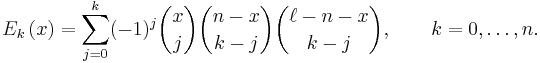Johnson scheme

In mathematics, the Johnson scheme, named after Selmer M. Johnson, is also known as the triangular association scheme. It consists of the set of all binary vectors X of length ℓ and weight n, such that 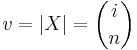$v=\left|X\right|=\binom{i}{n}$ .^[1]^[2]^[3] Two vectors x, y ∈ X are called ith associates if dist(x, y) = 2i for i = 0, 1, ..., n. The eigenvalues are given by

$p_{i}\left(k\right)=E_{i}\left(k\right),$

$q_{k}\left(i\right)=\frac{\mu_{k}}{v_{i}}E_{i}\left(k\right),$

where

$\mu_{i}=\frac{\ell-2i%2B1}{\ell-i%2B1}\binom{\ell}{i},$

and E_k(x) is an Eberlein polynomial defined by

$E_{k}\left(x\right)=\sum_{j=0}^{k}(-1)^{j}\binom{x}{j} \binom{n-x}{k-j}\binom{\ell-n-x}{k-j},\qquad k=0,\ldots,n.$

References

^ P. Delsarte and V. I. Levenshtein, “Association schemes and coding theory,“ IEEE Trans. Inform. Theory, vol. 44, no. 6, pp. 2477–2504, 1998.
^ P. Camion, "Codes and Association Schemes: Basic Properties of Association Schemes Relevant to Coding," in Handbook of Coding Theory, V. S. Pless and W. C. Huffman, Eds., Elsevier, The Netherlands, 1998.
^ F. J. MacWilliams and N. J. A. Sloane, The Theory of Error-Correcting Codes, Elsevier, New York, 1978.